אני חושב שהגישה הטובה ביותר היא לנסות להבין דוגמה קונקרטית:

בואו נסתכל על פיסת המישור האוקלידי המתואמת על ידי $ x ^ a = (x, y); a = 1,2 $ ברשת מלבנית נחמדה עם מדד אוקלידי. עכשיו נניח שאנחנו מגדירים טרנספורמציה $$ X (x, y) = x (1+ \ alpha y ^ 2) $$ $$ Y (x, y) = y (1+ \ alpha x ^ 2) $$ $ \ אלפא $ הוא רק קבוע, אותו ניקח בתור 5/512 - לצורך היכולת לצייר דיאגרמות. נקודה P עם קואורדינטות $ (x, y) = (8,8) $ ממופה לנקודה P 'עם קואורדינטות $ (X, Y) = (13,13) $.

תצוגה פסיבית

כאן אנו לא חושבים על P ו- P 'כנקודות שונות, אלא באותה נקודה ו- $ (13,13) $ הם רק הקואורדינטות של P במערכת הקואורדינטות החדשה $ X ^ a $.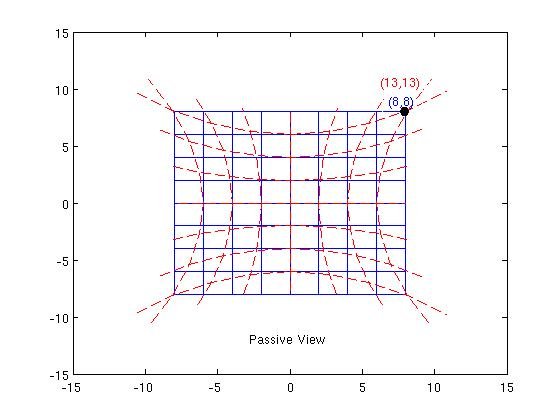

בתמונה, הקווים הכחולים הם קווי הקואורדינטות $ x ^ a = $ const והקווים האדומים הם קווי הקואורדינטות $ X ^ a = $ const. רכיבים מטריים בסעפת שלנו $ g_ {ab} (x) $ ממופים לערכים חדשים $$ h_ {ab} (X) = {\ frac {\ partial x ^ c} {\ partial X ^ a}} {\ frac {\ partial x ^ d} {\ partial X ^ b}} g_ {cd} (x) \ \ \ (1) $$ זה מייצג את אותו אובייקט גיאומטרי מאז $$ h_ {ab} (X) dX ^ a \ otimes dX ^ b = g_ {ab} (x) dx ^ a \ otimes dx ^ b $$

Active View

תיאור אחד של התצוגה הפעילה שמשתמשים בו לפעמים הוא נקודות "נעים סביב" (במובן מסוים אולי עדיף לחשוב רק על קשר בין נקודות, "זז" מרמז "ביחס לרקע כלשהו"). אז בדוגמה שלנו, היינו חושבים על הנקודה P כאילו היא "נמתחת" למיקום החדש P '. (מיקומים אלה הם ביחס למערכת הקואורדינטות הישנה $ x $).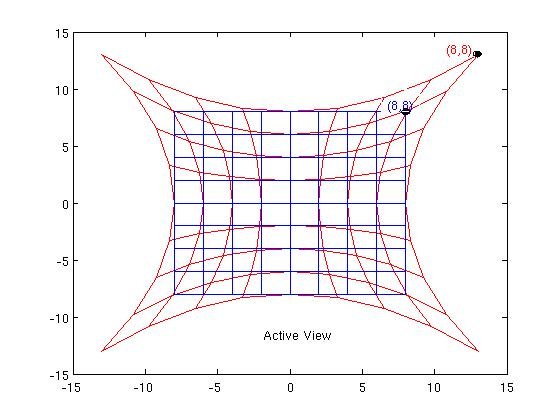

שורות הקואורדינטות הקבועות (הכחולות) $ x = $ נגררות גם יחד אל הקווים האדומים המוצגים בתרשים. אז הנקודה P שומרת על ערכי הקואורדינטות הישנים שלה $ (8,8) $ במיקומה החדש, כלומר $ (X, Y) = (8,8) $. המדד נגרר גם יחד (ראה למשל לוסאנה) על פי: $$ h_ {ab} (X) | _ {P '} \ dX ^ a \ otimes dX ^ b = g_ {ab } (x) | _ {P} \ dx ^ a \ otimes dx ^ b \ \ \ (2) $$ אז המדד האוקלידי הישן $ dx ^ 2 + dy ^ 2 $ הופך ל- $ dX ^ 2 + dY ^ 2 $ , כלומר עדיין אוקלידית בתרשים $ (X, Y) $ החדש - שום דבר לא השתנה. כך, למשל, הזווית בין הווקטורים האדומים $ \ frac {\ partial} {\ partial X} $, $ \ frac {\ partial} {\ partial Y} $ עדיין 90 מעלות, כפי שהייתה לגבי הווקטורים הכחולים $ \ frac {\ partial} {\ partial x} $, $ \ frac {\ partial} {\ partial y} $! הניחוש שלי הוא שזה מה שמתכוון וולד בשוויון הגופני - בדוגמה זו מדד אוקלידי נותר אוקלידי.

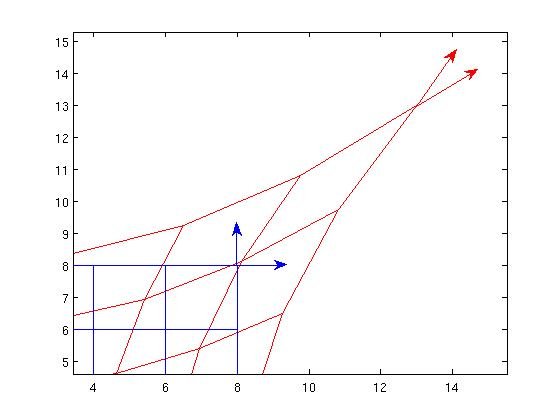
עכשיו, אם נסתכל על הווקטורים האדומים מנקודת מבט של המסגרת הכחולה, הם בטוח לא נראים אורתוגונליים *, אז מהנקודה הכחולה לראייה, זה יכול להיות רק מדד חדש שבו הווקטורים האדומים אורתוגונליים. כך שניתן לפרש דיפרומורפיזמים פעילים כמייצרים מדדים חדשים.

כעת נניח שיש לנו זמן מרחב - סעפת עם מדד שהניינר טנזור $ G _ {\ mu \ nu} $ נעלם. אם אנו משתמשים בדיפיומורפיזם פעיל, אנו יכולים ליצור את הגרירה של טנזור איינשטיין על ידי כלל המקביל ל- (2). כפי שדנו, אם נשווה את מדד הגרירה עם הישן באותם קואורדינטות, אנו רואים שיש לנו זמן מרחב עם מדד חדש. יתרה מזאת, זמן החלל החדש חייב להיות גם טנזור איינשטיין הנעלם - על ידי האנלוג של (2), העובדה שהוא נעלם במערכת הישנה פירושה שהוא נעלם במערכת החדשה ומכאן שגם הטנזור החדש שלנו שנוצר באינשטיין נעלם (אם טנזור נעלם. במערך אחד של קואורדינטות הוא נעלם בסך הכל).

* פשוט חישב את הווקטורים $ \ frac {\ partial} {\ partial X}, \ frac {\ partial} {\ partial Y} $ במונחים של $ \ frac {\ partial} {\ partial x} $, $ \ frac {\ partial} {\ partial y} $ ובדיקה האורתוגונליות שלהם באמצעות המדד האוקלידי המקורי.

אני חושב שוולד מבין את זה נכון וגליה ורובלי טועים. פעיל ופסיבי יש להם תחושות שונות מאוד, מכיוון ש- Active הוא נקודות זזות ופסיבי הוא פשוט בחירה מחודשת של קואורדינטות. אבל כל העניין של הקואורדינטות הוא שהם מתארים את הנקודות היטב, ולכן מיפוי הנקודות שווה ערך למיפוי הקואורדינטות. אין הבדל מהותי בין בלתי משתנה דיפרומורפיזם פעיל ופסיבי.

הדבר שיש ל- GR שאין תיאוריות אחרות אינו המושג "אין זמן חלל קודם" (ראה מיסנר תורן וילר), כלומר כל המבנה צריך להיות דינמי. שדות רקע קבועים אינם עולים בקנה אחד עם התיאוריה. אבל אני לא רואה איך זה קשור למחדל של דיפיומורפיזם. . לדוגמא, ניתן לשנות את המדד אך לא את העניין, או להיפך. אפשר גם לשנות את המדד, אבל אז לשמור על המדד שלא עבר שינוי. איזומטריה, למשל, משתנה בתרגום זמן, היא סטייה של המדד תחת סוג מסוים של דיפרומורפיזם. אך העובדה שאנו משווים את המדד שהופך לערך הלא-טרנספורמציה מבהירה כי אנו שומרים על משהו שלא עבר שינוי. זה לא אותו דבר כמו סטריאציה של דיפיומורפיזם, שמניחה שכל המבנה ממופה, ואף אחד מהמבנה הלא ממופה נשמר לשם השוואה.

אם לוקחים פתרון ואקום למשוואות איינשטיין, נכון שדיפומורפיזם פעיל יניב פתרון אחר. עם זאת, הגיאודזיה הלא ממופה לא תהיה באופן כללי גיאודזיה של המדד הממופה. כל מבנה לא ממופה יכול להיות לא תואם למשוואות איינשטיין הממופות, ולכן כדי לקבל פיתרון חדש עלינו למפות את הכל, כולל כל שדות האחרים (אם קיימים) וכן את כל קבוצות הנקודות (כולל גיאודזיה). בשלב זה מצאנו פיתרון חדש שהוא שווה ערך לפיתרון הישן, ואפשר היה למצוא אותו רק על ידי התבוננות בפתרון הישן בקואורדינטות חדשות.

כשאנחנו אומרים תרגום זמן זה. הפשטות היא סימטריה שמובילה לשימור אנרגיה, אין לזה שום קשר לסטיות הדיפרומורפיזם, למרות שתרגום הזמן הוא דיפרומורפיזם המיושם רק על המדד (או על כל דבר פרט למדד). סימטריה זו היא אמירה על טרנספורמציה של החומר ביחס למדד (הוא עדיין פיתרון), או הצהרה על טרנספורמציה של המדד ביחס לעצמו (הוא ללא שינוי). אנו יודעים שהכמות השמורה (אנרגיה) היא פיזית מכיוון שהיא יכולה לקחת ערכים שונים עבור תנאים התחלתיים שונים. זהו המשתנה של הפעולה (על מעטפת או כיבוי) כאשר הכל (מדד, כל שאר שאר התנאים ההתחלתיים) ממופה בכיוון t, והוא מתקיים גם כאשר אין איזומטריה (כמו במרחב מעוקל ברקע קבוע, או ב- GR). אין כמות שמורה מעניינת הקשורה אליו, ולכן זו סימטריית מד.

הייתי אומר וולד אומר את זה בצדק.

דיפיומורפיזם הוא מפה של הסעפת לתוכה, וזה טבעי לחשוב כנקודות נעות (רק חשוב על זה באופן ציורי: חצים בין שני עותקים של אותו סעפת). עם זאת, דברים נעים אלה אינם דבר בעל משמעות בגיאומטריה דיפרנציאלית - כל הנקודות בסעפת שוות ערך, במובן ששכונתם נראית כמו $ \ mathbb {R} ^ n $.

אם כן, התנועה שלדעתנו קשורה ל- diffeo יכולה להיחשב כתיוג מחדש של הנקודות: אם כל הנקודות שוות ערך, מה שאנו עושים כאשר אנו מסובבים אותן רק משנה את שמותיהן. זו הסיבה שאנו יכולים לנקוט בנקודת המבט הפסיבית שמבדילים משאירים נקודות ללא פגע ומשנים רק קואורדינטות.

במילים אחרות, הרעיון של העברת נקודה כרוך במבנה רקע: משהו נע ביחס למשהו אחר. מבנה רקע זה חסר בגיאומטריה דיפרנציאלית, ובגלל זה אנו יכולים לחשוב על אותה פעולה (diffeo) כמו העברת נקודות סביב או השארתן במקום שהן נמצאות ושינוי קואורדינטות.