כדי לענות על שאלה זו, נסה ליצור ערכת מצב.
יש לך שתי מסות $ m_1 $ ו- $ m_2 $. מעצם הגדרתו, למחתר על הכוחות יהיה המספר הראשון את אינדקס המסה הגורם לכוח וכשני את אינדקס האובייקט עליו מופעל כוח זה. מכיוון שאתה מעריך $ F_ {12} $ ואנו יודעים מהאינטואיציה הפיזית שלנו שכוח הכבידה הוא מושך, אתה יכול לצייר אותו מכוון ממרכז המסה 2 לכיוון מרכז המסה 1.
אם תנתח את ההגדרה של הווקטור $ \ vec {r} _ {12} $, תוכל לראות שהוא מוגדר כ:
$$ \ vec {r} _ {12} = \ vec {r} _2 - \ vec {r} _1 $$
ועל ידי יישום הכלל להוספת וקטורים, אתה יכול לראות שהוא צריך להיות מכוון ממסה 1 למסה 2. ואז, מנרמל אותו תוכל לקבל את הווקטור היחיד היחסי $ \ hat {r} _ {12} $.
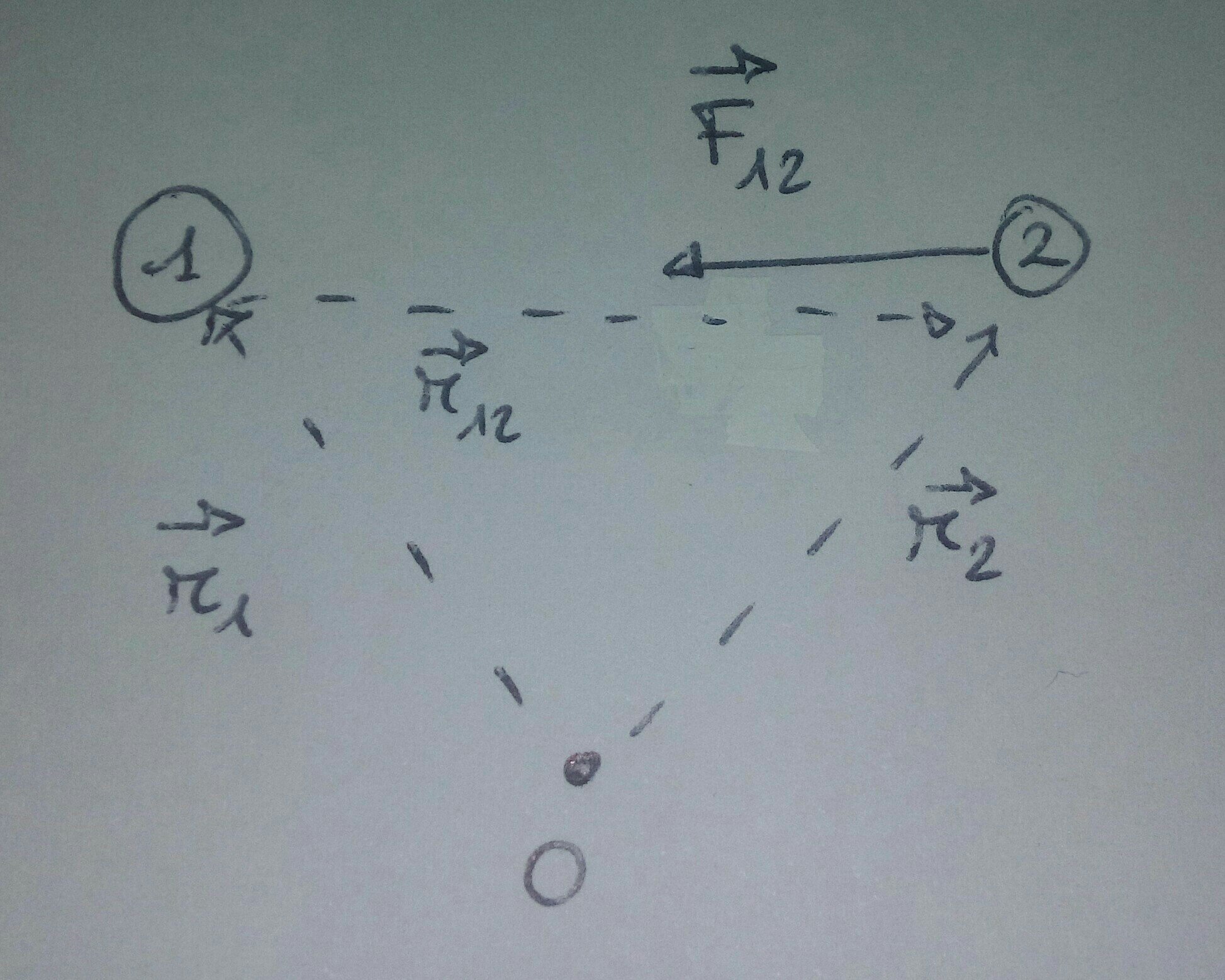
מהדיאגרמה, אז תוכל לראות ש- $ \ vec {F} _ {12} $ ו- $ \ vec {r} _ {12} $ נמצאים באותה קו, אך מכוונים לכיוונים שונים: סימן המינוס נובע מההבדל הזה.
הדבר תקף גם לספר שלך, שם אני מניח שהוא משמש במוסכמה אחרת לתיוג מנויי כוחות.
ניתן לכתוב את המשוואות הללו ללא סימן המינוס רק על ידי בחירת וקטור יחידני אחר, עם הכיוון הנכון. מצד שני, סימן המינוס רלוונטי מכיוון שהוא קשור באופן קונבנציונלי לכוחות אטרקטיביים. כמובן שכוח הכבידה תמיד מושך, אז סימן המינוס הזה תמיד קיים, אבל בכוחות מסוג אחר כמו כוח קולומב, מודול שלילי פירושו כוח מושך ואילו מודול חיובי פירושו דוחה, וסימן המודול מגיע מסימן ההאשמות.