בסדר, נתחיל בשאלתך הישירה. מכיוון ש $ d = vt $ הזמן שלוקח מרחק מסוים הוא ביחס הפוך למהירות שלך $ t \ propto v ^ {- 1} $, ולכן השינוי החלקי בזמן הוא פרופורציונלי לשינוי השבר השלילי במהירות שלך .

$$ \ frac {dt} {t} = - \ frac {dv} {v} $$ אז אם אנו רואים אופייני למהירות מהירה אופיינית של 65 קמ"ש והפרש של 5 קמ"ש, זה הוא שינוי חלקי של כ- 8%. אז נסיעה של 5 קמ"ש מהר יותר בכביש המהיר תגלח 8% מהזמן שלכם. אז אם הייתה לך שעה נסיעה, זה יתגלח 5 דקות.

גרור

אבל. בואו ננסה לשקול את העלות הנוספת של מעבר מהיר יותר. אם אתה הולך מהר יותר, גרירת הרוח גבוהה יותר, ולכן המכונית שלך זקוקה ליותר כוח כדי לשמור על המהירות. יותר כוח פירושו יותר אנרגיה, יותר אנרגיה פירושו יותר דלק, יותר דלק פירושו יותר כסף.

אם ניקח בחשבון רק את התרומה של התנגדות הרוח, אנו יודעים ש- $ F \ propto v ^ 2 $ למכוניות, ו ההספק הוא $ P = F v $ ולכן הכוח הנצרך על ידי גרור הולך כ- $ P \ propto v ^ 3 $. צריכת האנרגיה היא $ E = P t $, אז אם ניקח בחשבון כונן באורך קבוע, מכיוון $ t \ propto v ^ {- 1} $ יש לנו עבור תרומת גרירת האוויר, $ E \ propto v ^ 2 $. כעת, האנרגיה שאתה מקבל מדלק הינה פרופורציונאלית למספר הגלונים שאתה קונה, והמחיר מתדרג כמספר הגלונים כך ש $ \ text {דלק עלות} \ propto v ^ 2 $. כך שהשינוי החלקי בדלק הנצרך עקב גרירת רוח הוא: $$ \ frac {d (\ text {דלק עלות} _ {\ text {גרור}})} {\ text {דלק עלות} _ {\ text {גרור }}} = 2 \ frac {dv} {v} $$ לכן, עבור אותה עלייה של 8% במהירות, אתה משלם 16% נוספים בעלויות הדלק עקב אובדן גרירת אוויר.

באופן טבעי גרור אוויר אינו הדרך היחידה בה אנו משתמשים בדלק בכדי לשמור על מכונית פועלת, יש כל מיני הפסדים ברכב, החל מחוסר יעילות במנוע עצמו וכלה בחיכוך ברכיבי המנוע השונים וכו '. כמודל פשוט, בואו נגיד שההספק שמכונית צורכת הוא סכום גרירת האוויר ומונח קבוע שאינו תלוי במהירות: $ P \ sim \ alpha v ^ 3 + \ beta $ עבור כמה אפשרויות מתאימות של $ \ alpha $ ו- $ \ beta $ פירוש הדבר שצריכת האנרגיה שלנו עדיין תהיה $ E = P t $, אז בשביל נסיעה למרחק קבוע אנחנו מדברים $$ E \ sim \ alpha v ^ 2 + \ frac {\ beta } {v} $$. אנו יכולים לבדוק מודל זה מול נתונים ממחקר ממשלתי (איור מתוך ויקיפדיה: Fuel_economy_in_automobiles) כאשר למודל שלנו יש לנו $$ \ text {mpg} = \ frac {\ alpha} {v ^ 2 + \ frac {\ beta} {v}} $$

כאן הראיתי את הדמות כמו גם התאמה לדוגמא של המודל שלנו:

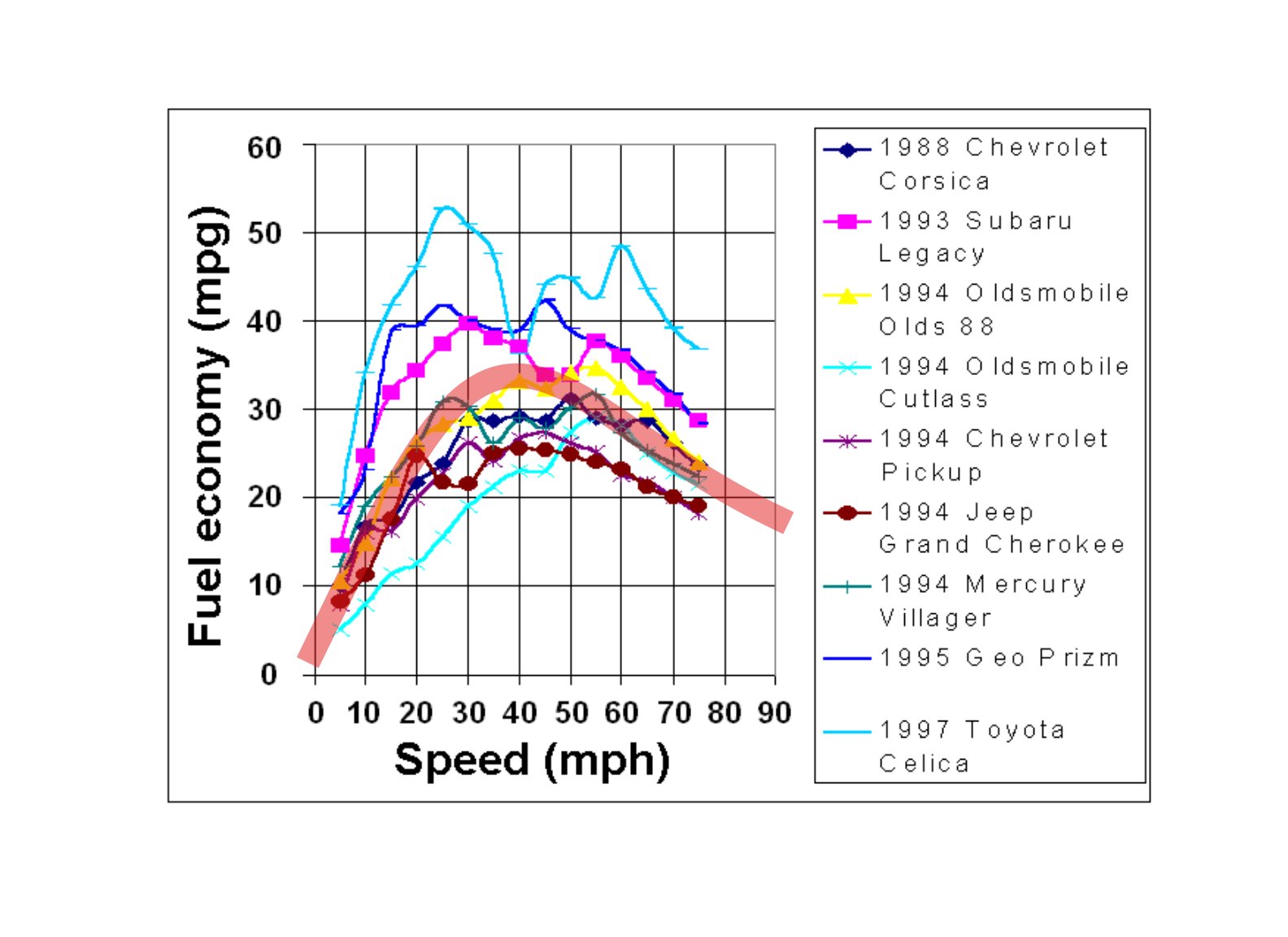
ההתאמה מכוסה באדום ותואמת $ \ alpha = 1.5 \ פעמים 10 ^ 5, \ beta = 1.28 \ פעמים 10 ^ 5 $. שימו לב שהמודל הפשוט שלנו מסתדר די טוב ומתאים למכונית שיש בה קמ"ש בכ- 25 מ"ג. שימו לב שבמהירויות גבוהות אנו רואים את קנה המידה שאנו מצפים עקב גרירת אוויר בלבד, שכן במהירות גבוהה עלויות התפעול שלנו נשלטות על ידי התנגדות אוויר, אך היה שימושי ליצור את המודל הפשוט ולעשות את ההתאמה במקרה זה מכיוון שהאזור העניין הוא באזור החפיפה.

לשעה

עכשיו כשאנחנו יודעים איך היעילות של המכונית שלנו משתנה עם המהירות, בידיעה שמחיר הדלק הממוצע הוא $ 3.752 $ / גלון (מ- wolfram alpha) אנו יכולים לחשב את העלות להפעלת מכונית ממוצעת במהירות נתונה:

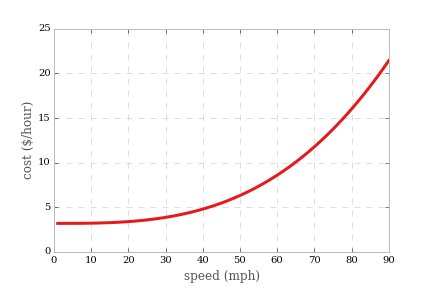
במיוחד אנו יכול לחשב את העלות הנוספת לשעה לעלייה במהירות של 5 קמ"ש כפונקציה של מהירות:

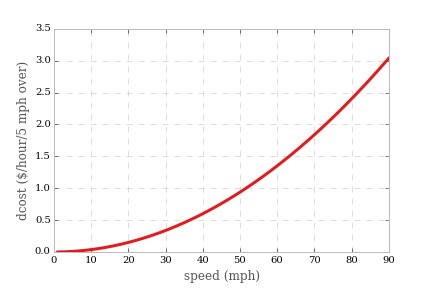
לכל 10 מיילים

כאן הראיתי את עלויות התפעול כפונקציה של זמן הנסיעה, בכדי לתת עלויות לשעה, מה שלדעתי שימושי לכוננים ארוכים יותר ולמשהו שאנשים מצליחים להתמודד איתו מאזורים אחרים בחיים.

אם במקום זאת נרצה לראות זאת כפונקציה של מרחק הנסיעה, נוכל להסתכל על יעילות הרכב כעלות הנסיעה של 10 ק"מ כפונקציה של מהירות.

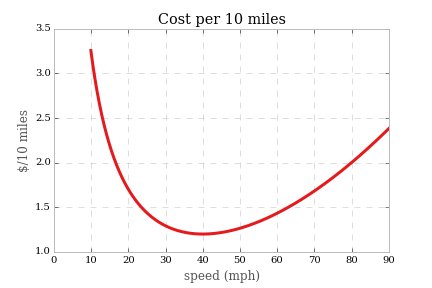
או שנוכל לשקול שוב את השינוי שנוצר בעליית מהירות של 5 קמ"ש למרחק נסיעה קבוע.

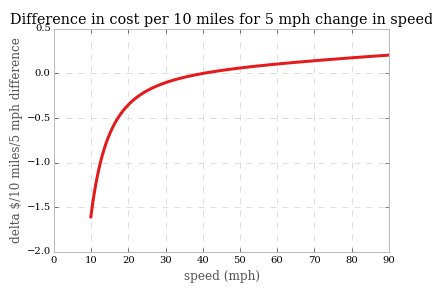
לאן כאן זה הופך להיות ברור כי למרחק נסיעה קבוע, כל עוד אתה עובר פחות מ -40 מייל לשעה (אשר עבור המודל שלנו היה מהירות יעילות הדלק המקסימלית, ומשתנה לפי מכונית, אך נראה שהנתונים מצביעים על כ -40 קמ"ש על כל הלוח) , אתה תמיד יכול להצדיק מהירות במהירות של 5 קמ"ש מבחינה כלכלית גרידא, אך במשהו כמו מהירויות בכבישים מהירים זה עולה לך עוד 15 סנט לערך לכל 10 מיילים לעבור 5.

רמזורים

אז עד לא שקלנו את היעילות של נהיגה במהירות מופרזת מנקודת מבט כלכלית בגבול שבו אנו נוסעים ללא הפרעה בהמשך הדרך. כפי שאנשים ביקשו בתגובות, בואו ננסה להבין עד כמה יעילות מהירות מהירה בסביבה יותר עירונית. זו בעיה קשה לטפל בה, שכן ברמזורים יכולים להיות בקרים די מורכבים. בפרט, באזורים מסוימים ישנם גלים ירוקים שבהם האורות נועדו לאפשר לאנשים הנוסעים במהירות הנכונה לעבור ללא הפרעה לאורך קטעי דרך ארוכים. ברור שבמקרה זה היית רוצה לנסוע במהירות הגל הירוק והמהירות לא תעזור לך ולמעשה תפגע בך.

אך בקרי רמזור מתוחכמים אינם כל כך נפוצים מחוץ לערים גדולות ועשירות. אז בואו ננסה לאמץ קירוב מסוג פרה כדורית לרמזורים ונניח שרמזורים הם עצמאיים ופשוט פועלים על איזה מחזור קבוע של ירוק ואדום. $ p $ יהיה שבריר הזמן שהרמזור הממוצע ירוק, $ \ tau $ יהיה באור של נורה אדומה, $ d $ יהיה המרחק הממוצע בין הרמזורים. אם הנורות כולן פועלות באופן עצמאי, ניתן לתכנן את חלוקת זמני ההמתנה בהגיענו לאור כ $$ P (t) = p \ delta (t) + \ frac {1} {\ tau} (1 - p) \ quad 0 \ leq t \ leq \ tau $$ או במילים, עם הסתברות $ p $ אנחנו בכלל לא צריכים לחכות, אחרת זמן ההמתנה שלנו יהיה אחיד עד $ \ tau $. התפלגות זו כוללת ממוצע ושונות $$ \ mu = \ frac {\ tau} {2} (1 - p) $$$$ \ sigma ^ 2 = \ frac {\ tau ^ 2} {12} (1 - p) (3 p + 1) $$

כעת, אם ניסע לחסימות של $ N $, יהיה לנו למשך הזמן הממוצע שלוקח $$ \ langle t \ rangle = N \ left (\ frac { d} {v} + \ frac {\ tau} {2} (1 - p) \ right) $$$$ \ sigma ^ 2_t = N \ frac {\ tau ^ 2} {12} (1- p) ( 3 p + 1) $$ שם הוספנו בזמן הנסיעה בין האורות עצמם.

כך, למשל, עם $ d = 1/10 $ מייל בין האורות בממוצע, $ \ tau = 30 $ שניות ו- $ p = 0.65 $ אנו מקבלים עבור מהירות עירונית ממוצעת כפונקציה של מהירות המטרה: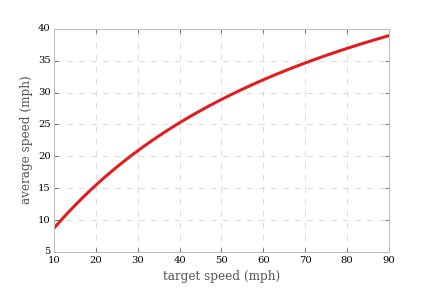

אז למהירות יעד של כ 45 קמ"ש לכביש ראשי בעיר , אנו מקבלים במהירות ממוצעת משהו כמו 28 קמ"ש, שנראה שמסכים בינוני עם תצפיות.

עכשיו, כפי שדגמנו את זה, אם תאיץ במהירות תגיע לשם מהר יותר, אבל מה שעלינו להשוות מול זה השונות המהותית שמציגה הרמזורים, ואפשר לטעון שמהירות של 5 קמ"ש מעלה היא באמת רק שווה את זה אם הרווחים שאתה מקבל בתזמון גדולים יותר מהשינויים הטבעיים בזמנים שהיית נותן את האורות, אחרת בקושי תבחין בהשפעה. אז בפרט, אנו יכולים להשוות את ההפחתה החלקית בזמן הנסיעה שלך לעלייה של 5 קמ"ש, לעומת השינוי החלקי בזמן הנסיעה שלך עקב השונות המהותית בגלל תזמוני האור האקראיים $ (\ sigma / \ mu) $ עבור שונים מספר חסימות. אנו משיגים:

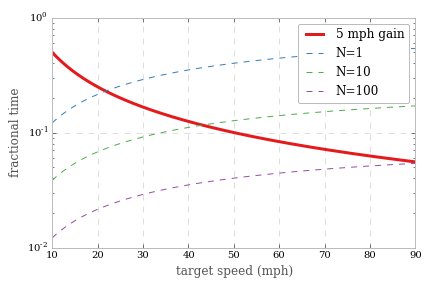
כאן הקו המוצק מראה את השינוי החלקי בזמן הנסיעה שלך שתקבל על ידי מעבר של 5 קמ"ש מעל מהירות היעד בתחתית. שים לב שהוא מתמקד כ- $ 1 / v $ בדיוק כמו החלק העליון של ההודעה. הקווים המנוקדים מראים שינוי חלקי בזמן הנסיעה הנגרם על ידי וריאציה של 1 סיגמא בהתנהגות הרמזורים, למספר חסימות שונות. שימו לב כי בסביבות 40 קמ"ש, הזמן שבו הייתם מתגלחים על ידי נסיעה של 5 קמ"ש הוא דומה לשינויים הטבעיים שהייתם מצפים בזמני הנסיעה בגלל המזל שלכם עם הרמזורים אם אתם נוסעים 10 רחובות, ושני אלה נמצאים בערך ברמה של 10%. בשלב זה מתחיל להיות קשה להצדיק מהירות מופרזת מכיוון שקשה להבחין בהשפעה שלה על השונות הטבעית. אבל שים לב שאם אתה נוסע למרחק ארוך יותר, יש רווח ברור שניתן במהירות מופרזת, מכיוון שהשינויים בזמן הנסיעה מתחילים להיות מודחקים באמצעות ממוצע. מהצד השני, לנסיעות קצרות מאוד של כמה רחובות, הווריאציות בזמן הנסיעה שלך הניתן על ידי המזל שלך באורות שולטים לחלוטין על כל רווח שתקבל על ידי מהירות מהירה.

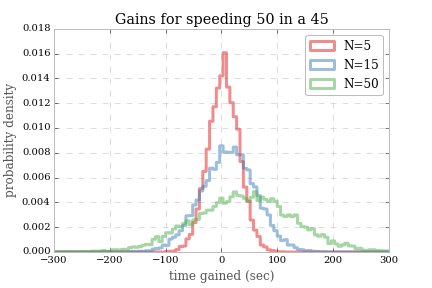
כאן סימילתי נסיעה של 5, 15 או 50 חסימות על פי המודל שלנו, הן 45 קמ"ש והן 50 קמ"ש. רצתי את הסימולציה 10,000 פעמים וכאן אני מראה את הזמן שנצבר ממהירות במהירות בניסויים שונים. כאן אנו באמת יכולים לראות שאין רווחים ניכרים לעלות על 5 מעל 5 בלוקים, זה נשטף לחלוטין על ידי המזל שלנו עם האורות, אבל שינוי ניכר בזמן הצפוי שלנו מעל 50 בלוקים.

תוספת: בחנתי מודל מציאותי יותר של הפסדי חשמל במכוניות ב תשובה עדכנית יותר

מלבד ההשפעה על נהג אחד, אתה יכול לשקול את ההשפעה על התנועה באופן כללי, זה מה שקורה כאשר כולם פורצים את הגבלת המהירות. בכל הנוגע לדינמיקה של נוזלים, תופעות הלוואי של המהירות שלך (אם בכלל) מורגשות על ידי האנשים שמאחוריך.

מרחק התגובה עולה באופן ליניארי עם המהירות, אך מרחק העצירה חייב לכלול מונח פרופורציונלי ל ריבוע המהירות, שכן עם האטה מתמדת אנו יודעים ש- $ v ^ 2 = u ^ 2 + 2as $

מרחקי עצירה "רשמיים" הם ממילא סממנים, מכיוון שגם בתנאי נהיגה קבועים הם אינם מהווים חשבון שונות בין מכוניות. עם זאת, ממשלת בריטניה מגדירה "מרחק בלימה" כ- $ v ^ 2 * k $ כאשר $ k $ הוא 0.015 מטר / קמ"ש ² [אני יודע, גם אנחנו לא לגמרי במערכת המטרית] ואז עיגול אותו.

• מרחק עצירה כולל ב -65 קמ"ש: 83 מטר
• מרחק עצירה כולל ב -70 קמ"ש: 96 מטר

משמעות הדבר היא אם מכוניות מפרידות את עצמן לפי מרחק העצירה (מה שבאמת לא, אבל אם ), עליית המהירות של 7.7% מגדילה את ההפרדה ב -15.7%, כך שבזמן נתון 8% פחות מכוניות עוברות כל נקודה נתונה לנתיב תנועה. תנועה מהירה יותר מפחיתה את קיבולת הכביש.

למעשה מכוניות אינן מפרידות את עצמן על ידי מרחק העצירה (או אפילו על ידי חלק קבוע ממנו), אז מה שקורה בפועל הוא איזו פשרה בין מופחת יכולת, וכל המערכת מסתמכת יותר על זמני התגובה של אנשים, שאינם אמינים לחלוטין. זה קצת יותר מסוכן, אבל גם בהנחה שלא מתנגשים זה עדיין משפיע על ההתקדמות הכללית של התנועה. נהגים רבים יותר יצטרכו להחתים על העוגנים כאשר האדם שמולם עושה משהו מפתיע מכיוון שהם מתקרבים באופן יחסי למרחק התגובה הטהור שלהם.

זהו אזור שבו נכנסת דינמיקת הנוזל. בלימה פתאומית גורמת לאדם שעומד מאחוריך לעשות את אותו הדבר, מה שהופך זרימה חלקה (למינרית) של תנועה לזרימה סוערת. הרבה פחות פחות תעבורה עוברת את אותה נקודה, והתנועה מגבה מאחוריה. אפילו נאמר כי עצם החלפת נתיבים בתנועה צפופה מהירה יש סיכוי מסוים לגרום לתנועה להיעצר זמן מה אחר כך וכמובן למכוניות רבות מאחוריך. ברגע שנוצר אחד מהפקקים הספונטניים האלה ללא סיבה, הם נמשכים די הרבה זמן ומאטים את המסע של כולם. אין לי נתונים על גודל ההשפעה.

כל מה שאמר, אני לא חושב ש 65/70/75 קמ"ש הוא האזור הקריטי בתנועה העמוסה. בריטניה משתמשת במגבלות מהירות משתנות בזמן אמת יותר כמו 50 קמ"ש כדי לשפר את התפוקה הכוללת בכבישים עמוסים. כך שההבדל בין 65 לכולם ל -70 לכולם הוא ככל הנראה זניח, מכיוון שגיל 65 כבר גורם למערבולות רבות כאשר הכביש "מלא". סביר להניח שתמצא שזה כמעט בלתי אפשרי במגבלת מהירות זמנית לבצע מהירות שאינה זהה לכולם, וזה סוג של הרעיון.

[עריכה: עבור כלכלנים, זהו שוק לא יעיל. . כל נהג מרוויח מנהיגה מהירה מעט יותר, אך מפסיד אם כולם נוהגים מעט מהר יותר. הם "צריכים" כולם להתכווץ לעמוד במהירות מסוימת מתחת לגבול הקבוע, אך אין להם את האמצעים לעשות זאת. רק לבעל הדרך (הממשלה) יש את המידע לבחור במגבלה "טובה יותר" (קרוב יותר לנקודה אופטימלית של פארטו) או באמצעים להעביר אותה לנהגים. כבישים פרטיים היפותטיים יכולים כמובן גם להטיל על נהגים כל מה שהם בחרו ב- T&C, כולל לאסור או לגבות אותם בגין אי ביצוע אמצעי נגד עומס, וניתן לטעון ש אולי מגיבים יותר למשוב הלקוחות מאשר הממשלה היא: -)]

אם המהירות המותרת היא 60 קמ"ש, ייקח 60 דקות לעבור 60 מייל. כדי לעבור את אותם 60 מיילים במהירות 65 קמ"ש, זה לוקח 55.4 דקות. חיסכון בזמן של 4.6 דקות. האם באמת כדאי לזרז אם כל מה שאתה הולך לחסוך הוא כמה דקות (אפילו פחות למרחקים קצרים יותר).

למודלים של דינמיקת נוזלים יכול להיות ערך מעשי באזורים עמוסים בכבדות, אך אז אינך יכול להאיץ, ולחסוך כמה סיביות קצרות אקראיות לאחר אותות תנועה, מה שהופך אותו ללא רלוונטי. אני מניח שהם יותר מודלים להפצת תנועה, כבישים קטנים יותר ימשכו יותר תנועה אם הלחץ הנגדי (העומס) יעלה בצינור הראשי (כביש).

זה באמת תלוי אם אתה יכול לשמור על הממוצע מהירות גבוהה יותר, וזה קשה באופן לא אינטואיטיבי. אם אתה נוהג רחוק, נסיעה מהירה יותר יכולה לעשות הבדל גדול. בנסיעות של 400 מייל בדרכים של 60 קמ"ש אפילו קבוע +5 קמ"ש יחסוך כחצי שעה, בהנחה שתוכלו לשמור על הממוצע. אני לא יודע אם המשאיות שלך מוגבלות ל -50 קמ"ש (80 קמ"ש), אך עקיפת משאית בהתחלה עשויה לחסוך גם 1 שעה 20 דקות.

באזורים צפופים חלקית שבהם אתה יכול לנהוג מדי פעם ב + 5, אבל אז מבלים את אותו שיעור זמן מאחורי מישהו בגבול, המהירות הממוצעת נמוכה מ -2.5. תגיד, הנסיעה שלך היא 25 מיילים, ואתה מבלה בסך הכל 15 דקות ב 50 קמ"ש (מכסה חצי מהמרחק), ובין הקטעים האלה נוסעים במהירות 55 קמ"ש, אתה מגיע ליעד רק דקה 20 שניות קודם לכן, והממוצע הוא מתחת ל -52.4 קמ"ש (במציאות אפילו קצת יותר נמוך, כי המהירות שלך לא משתנה באופן מיידי 50-> 55.

אם המגבלה עדיין נמוכה יותר, וישנם צמתים מבוקרי אותות, התנאים המקומיים מתחילים להיות חשובים יותר. אם אתה יודע שהמהירות הנוספת בחלק מסוים תחסוך לך נורה אדומה אחת, או שזה קורה במקרה (או על ידי הימצאות שם רגע לפני שהאור מתחלף, או על ידי מיקום טוב יותר בתור כדי שלא תצטרך לעצור פעמיים ), ייתכן שתחסוך 30-90 שניות נוספות לכל צומת כזה. אם אותה נסיעה של 25 מייל נמצאת באזור 40 קמ"ש, ואתה עוצר ב -10 נורות אדומות למשך 40 שניות בכל פעם, המהירות הממוצעת שלך היא 33.9 (בהנחה ששינוי מהיר מיידי). אם היית בן 45 ונמנע משלושת הנורות האדומות האחרונות, הממוצע היה תלוי במרחק מהאותות השביעיים ליעד; עם אותות מרווחים באופן שווה, הממוצע יכול להיות 41.6 קמ"ש - בהנחה שהייתם צריכים לחכות יותר (65 שניות, כך שייתכן שכביש כזה יכול להתקיים) בשבעת האותות הראשונים, כלומר הייתם מעבירים את אותו מחזור האות. זה 44 דקות לעומת 36 דקות. במקרה קיצוני, אם האותות מספיק רחוקים זה מזה ו- +5 עוזר לך למנוע עצירה בכולם, היית מגיע ליעד שלך תוך קצת יותר מ- 33 דקות. בדרך כלל, עם זאת, הם מנסים לתזמן את האותות קרוב אחד לשני, כך שכל מהירות "סבירה" לא תעביר אותך דרך אותות רצופים מהר יותר מאלה שמדביקים אותך במחזור הירוק הבא מהאותות הקודמים. כמו כן, אם הולך +5 היה מעביר אתכם בשלושה אותות אחרים בדרך, תלוי איך או אם התזמון שלהם מחובר ביניהם וכמה זמן המחזורים הם, האם הבחור שהולך בן 40 יהיה שם אפילו באותו מחזור האות של אותות התנועה האחרונים + הפרש הזמן מאותם אותות לנקודת הקצה.

[מבוא לא ממש עונה על השאלה: נשמע כמעט כמו שאלה של פילוסופיה קלאסית. כדי להפוך אותו, אולי תשאל אם כדאי לנסוע במהירות המותרת של 5 קמ"ש לאט יותר. ו -5 קמ"ש לאט מזה. או שאתה צריך פשוט ללכת? "]

התשובה המקובלת מחשבת את החיסכון בזמן ואת עלות הדלק.

בענף התעופה, זה פורמלי על ידי הגדרת" מדד עלויות התעופה ". זה מחיר היחס זמן 'חלקי' מחיר דלק 'ומהווה קלט למחשב ניהול הטיסות.

אז, אם מתעלמים מהסוגיות המשפטיות סביב מגבלת המהירות, משוואת הגרר פירושה שככל שמחיר הזמן גבוה יותר, ככל שאנחנו צריכים ללכת מהר יותר.

נראה לי שדבר זה נוגע לנהיגה ברכב.

חיסכון של 5 דקות כדי להגיע למסיבה הפועלת כל הערב שונה מחיסכון של 5 דקות ולכן כמו להגיע לראיון עבודה בזמן, או להביא מישהו לבית חולים.

נוסף על כך נושאי הבטיחות. מרחק הפריצה הוא בערך מהיר, ולכן עליית מהירות של 10% פירושה 20 %% עליית מרחק הבלימה. התור מתייחס לשאלתך לגבי "לאן אתה ממהר". מהירות רק כדי לעבור דרך אורות לא יכולה להיות המקום הבטוח ביותר לעשות זאת.