Edit: אני משאיר את זה בגלל שיש מאמץ שהושג להציג כיצד מתקבלות החלטות בערוצים מסובכים. התשובה הפשוטה של @ atlas-insider מבהירה את הנקודה הכללית שה- OP שואלת.
מתוך מדגם נייר ATLAS המופיע בתגובות
S חיפוש אחר סופר-סימטריה ב $ \ sqrt {s} = 13 \ \ rm TeV $ במצבים סופיים עם סילונים ושני לפטונים מאותו סימן או שלושה לפטונים עם גלאי ATLAS
חיפוש אחר חלקיקים על-סימטריים המיוצרים חזק נעשה באמצעות חתימות הכוללות סילונים אנרגטיים מרובים ושני לפטונים מבודדים ( $ e $ או $ \ mu $ ) עם אותו מטען חשמלי או לפחות שלושה לפטונים מבודדים. החיפוש משתמש גם בסילונים מתויגים $ b $ , חסרים תנע רוחבי ותצפיות אחרות כדי להרחיב את רגישותם. הניתוח משתמש במדגם נתונים של התנגשויות פרוטון-פרוטון ב $ \ sqrt {s} = 13 \ \ rm TeV $ שנרשם עם גלאי ה- ATLAS ב- Collider Hadron הגדול ב- 2015 המקביל לסהירות משולבת כוללת של 3.2 $ \ \ rm fb ^ {-1} $ .
רואים שמדובר בחיפוש ספציפי שצריך כמטוסי סילון ולפטונים.
הדמיות מונטה קרלו משמשות רבות כדי למצוא את ההסתברות לזיהוי שגוי של מועמדים עקב מטוסי סילון המגיעים מתגובות אחוריות לזו המבוקשת ואת יכולת הלפטונים הנובעים מריקבונות של ערוצים לא רצויים, עד לערוץ הנחקר.
לאחר זיהוי האובייקט, נפתרות חפיפות בין אובייקטים. כל סילון העוצר מרחק $ \ Delta R_y = \ sqrt {(\ Delta y) ^ 2 + (\ Delta \ phi) ^ 2} = 0.2 $ של אלקטרון המועמד מושלך, אלא אם כן למטוס יש ערך של $ \ rm MV2c20 $ מבדל גדול מהערך המקביל לכ- $ 80 $ span>% $ b $ יעילות תיוג, ובמקרה כזה האלקטרון מושלך מכיוון שהוא ככל הנראה מקורו בסמיפטון $ b $ ריקבון האדרון. כל אלקטרון שנותר בתוך $ \ Delta R_y = 0.4 $ של סילון מושלך. מונחים בתוך $ \ Delta R_y = 0.4 $ של מטוס מוסרים גם הם. עם זאת, אם למטוס יש פחות משלושה מסלולים נלווים, המואון נשמר והמטוס מושלך במקום זאת כדי למנוע חוסר יעילות עבור מונונים בעלי אנרגיה גבוהה שעוברים אובדן אנרגיה משמעותי בקלורימטר.
בחיפוש הספציפי הזה יש מדדים להחליט מתי יש לאדם אירוע על-סימטרי מועמד, שהוחלט מתוך הדמיית מונטה קרלו של האירועים הרצויים בגלאי. מטוסי סילון או אלקטרונים נדחים אם הסבירות שהם מגיעים מרקע גבוהה.
אלקטרוני האות חייבים לעמוד בדרישת זיהוי מבוססת סבירות הדוקה [57, 58] ויש להם $ | \ eta | <2 $ כדי להפחית את ההשפעה של טעינת מטען אלקטרונים -זיהוי. Muons signal חייבים למלא את הדרישה של $ | d_0 | / \ sigma (d_0) <3 $ . על המסלול המשויך ללפטונים האותיים להיות בעל פרמטר השפעה רוחבי ביחס לקודקוד הראשי המשוחזר, $ z_0 $ , המספק את $ | z_0 \ sin \ theta | <0.5 \ \ rm mm $ . דרישות בידוד מוחלות הן על אלקטרוני האות והן על המוניונים. הסכום הסקלרי של $ p _ {\ rm T} $ . רדיוס חרוט בידוד המסלול לאלקטרונים (muons) $ \ Delta R_ \ eta = \ sqrt {(\ Delta \ eta) ^ 2 + (\ Delta \ phi) ^ 2} $ ניתן על ידי הקטן מ- $ \ Delta R_ \ eta = 10 \ {\ rm GeV} / p _ {\ rm T} $ ו- $ \ Delta R_ \ eta = 0.2 (0.3) $ , כלומר קונוס בגודל 0.2 $ (0.3) $ ב- נמוך $ p _ {\ rm T} $ אך צר יותר עבור $ p _ {\ rm T} $ לפטונים. בנוסף, במקרה של אלקטרונים האנרגיה של אשכולות אנרגיה קלורימטר בחרוט של $ \ Delta R_ \ eta = 0.2 $ סביב האלקטרון (לא כולל התצהיר מה האלקטרון עצמו) חייב להיות פחות מ $ 6 $ % מהאלקטרון $ p _ {\ rm T} $ . אירועים מדומים מתוקנים על מנת להסביר הבדלים מינוריים בהדק לפטון, יעילות שחזור וזיהוי בין נתונים לבין סימולציית MC.
התוצאה הסופית היא האפשרות לקבוע מגבלה לגילוי הערוץ העל-סימטרי הנחקר.
קבלה או דחייה של לפטון או סילון להגדרת הטופולוגיה של התגובות שנחקרו, במקרה זה חיפוש אותות על-סימטריים, תלויה במידה רבה בערוץ הספציפי.זה תלוי בלימוד המתמטיקה של הקינמטיקה הצפויה מהערוצים הנחקרים.
יכול להיות שמוצאים מספרים סטנדרטיים לדחייה, זאת בשל העובדה שדיוק הגלאי נחקר בכלים דומים של מונטה קרלו, אך עדיין אין זו דחייה כללית מבלי ללמוד היטב את ההפצות לכל ערוץ תחתללמוד.
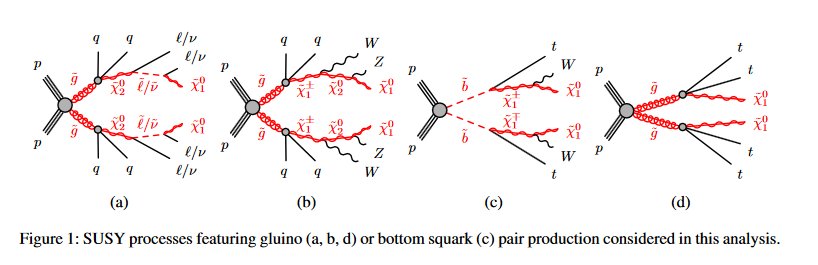
אז זה לא שהאלקטרון יכול לזייף סילון, מכיוון שמטוסים מתחילים יחד עם מסלול האלקטרונים בגלאי המעקב.זה יכול להיות אלקטרון ממטוס לא רצוי או לפטון מהתפרקות תהודה נמוכה יותר או נמוכה יותר, למשל.הדבר נכון גם לגבי מטוסים.אחד מחפש אחר טופולוגיות הסילון והלפטון המוצגות באיור המועתק למעלה, ומפתח אמצעי דחייה המתאימים לערוצים.